Contenido
El sistema de coordenadas cartesianas es la manera más habitual de ordenar la posición de los elementos en el plano y en el espacio. En este tema nos centraremos en los sistemas en el plano (2 dimensiones)
Definición: sistema de coordenadas cartesianas en el plano está formado por dos rectas perpendiculares (eje vertical OY, eje horizontal OX) que se cortan en un punto denominado origen. Cada uno de los dos ejes está escalado de forma que la distancia entre dos naturales consecutivos es la misma. La parte derecha (respecto al origen) del eje OX es el semieje positivo siendo la izquierda el negativo. En el eje OY la parte positiva es la de arriba del origen siendo la negativa la inferior
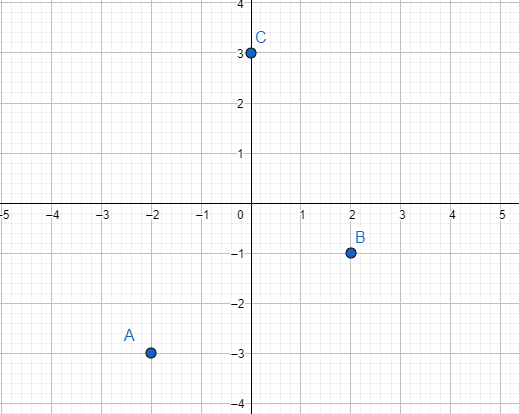
Definición: un punto P en el plano nos describe una posición, viene definido por dos coordenadas P(x,y), siendo las proyecciones del punto en los ejes OX y OY. Los puntos se escriben con mayúsculas y las coordenadas se escriben a continuación de la letra sin igual entre ambas.
Ejemplos: A(-2,-3), B(2,-1), C(0,3)
Definición: vector fijo ![]() entre dos puntos A (origen) y B (extremo) es un segmento orientado caracterizado por:
entre dos puntos A (origen) y B (extremo) es un segmento orientado caracterizado por:
- Dirección o recta que le contiene o cualquiera paralela
- Sentido u orientación del vector de A a B
- Módulo o longitud del segmento, se denota como |
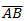 |
| - Origen (el punto A)
Coordenadas del vector fijo: el vector ![]() caracterizado por dos coordenadas
caracterizado por dos coordenadas ![]() =(x,y), donde x indica las unidades que avanza en el eje horizontal e y las unidades de avanza en el eje vertical. Las coordenadas se obtienen restando las coordenadas del extremo menos la del origen, si A(xa,ya) y B(xb,yb) à
=(x,y), donde x indica las unidades que avanza en el eje horizontal e y las unidades de avanza en el eje vertical. Las coordenadas se obtienen restando las coordenadas del extremo menos la del origen, si A(xa,ya) y B(xb,yb) à ![]() =(xb-xa,yb-ya).
=(xb-xa,yb-ya).
Ejemplo: veamos gráficamente el vector ![]() :
:

Vemos en este ejemplo ![]() =(4,2), vemos que avanza 4 unidades a la derecha y 2 hacia arriba.
=(4,2), vemos que avanza 4 unidades a la derecha y 2 hacia arriba.
El módulo del vector se denota como |![]() |. Para calcular el módulo de un vector
|. Para calcular el módulo de un vector ![]() =(x,y)=(xb-xa,yb-ya) aplicamos el teorema de Pitágoras:
=(x,y)=(xb-xa,yb-ya) aplicamos el teorema de Pitágoras:
![]()
Nota: ![]() es decir mismo módulo dirección, pero sentido opuesto.
es decir mismo módulo dirección, pero sentido opuesto.
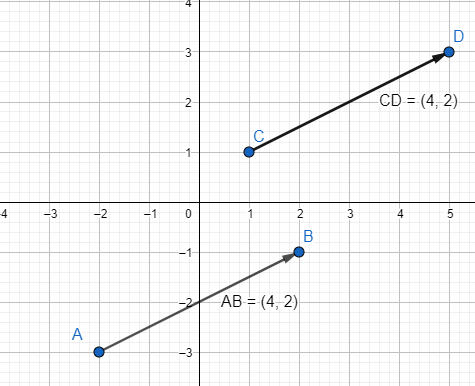
Definición: vectores equipolentes son los que tienen misma dirección, sentido y módulo, lo único que cambia es el origen del vector. Las coordenadas son las mismas en todos los vectores equipolentes.
Ejemplo: A(-2,-3), B(2,-1), C(1,1), D(5,3) , ![]()
Definición: vector libre es el conjunto de todos los vectores equipolentes, se suelen denotar con una letra minúscula con vector arriba. A la hora de representarlos se suele tomar el vector cuyo origen está en el origen de coordenadas.
Ejemplo el vector ![]() es el conjunto de todos los vectores con coordenadas (4,2) es decir que avanzan 4 unidades en el eje x positivo y 2 unidades en el eje y positivo.
es el conjunto de todos los vectores con coordenadas (4,2) es decir que avanzan 4 unidades en el eje x positivo y 2 unidades en el eje y positivo.
