En este apartado veremos las posiciones relativas entre dos rectas, que pueden ser:

• Secantes: se cortan en un punto
• Paralelas: si no tienen ningún punto en común (misma pendiente, o vector director)
• Coincidente: son la misma recta (dos puntos en común).

La posición relativa la hemos estudiado indirectamente cuando veíamos las soluciones de un sistema de ecuaciones lineales, ya que:

• Rectas paralelas: si dos rectas son paralelas no se cortan y no tienen solución. Sistema incompatible
• Rectas secantes: si son secantes se cortan en un punto y por tanto una solución. Sistema compatible determinado
• Coincidentes: si son coincidentes son la misma recta e infinitas soluciones. Sistema compatible indeterminado.

Si expresamos las dos rectas en forma general, tenemos

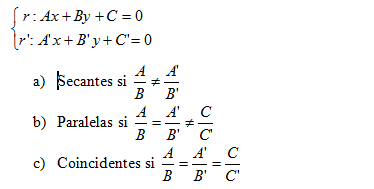
Si tenemos las rectas en otras formas distintas de la expresión general podemos ver su posición relativa a partir de conocer sus pendientes o sus vectores directores:

1. Si son secantes se cumple: sus pendientes son distintas: m₁≠m₂  y se cumple también que los vectores directores no son iguales o proporcionales: v₁≠k·v₂

2. Si son paralelas o coincidentes: sus pendientes son iguales m₁₌m₂ y los vectores son proporcionales v₁₌k·v₂. 

a. Si son coincidentes tienen algún punto en común

b. Si no son coincidentes ningún punto es común.