Ecuación continua:

En las dos ecuaciones paramétricas de r lo que vamos a hacer es eliminar la t del sistema y relacionar “y” con “x” como si fuera una función.

Despejando t de la ecuación en paramétricas tenemos una relación entre las variables x e y:

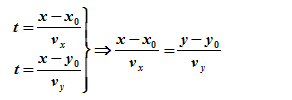
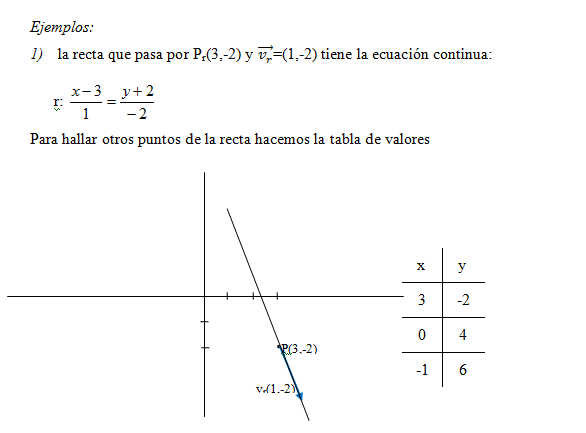
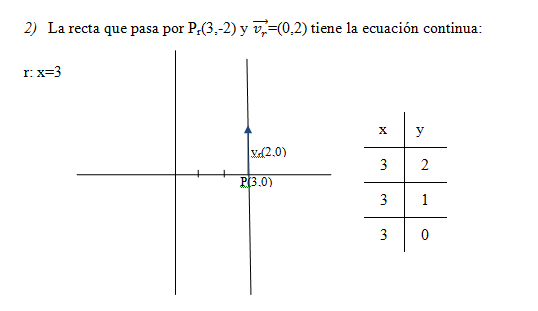
La ecuación de la recta,r, que pasa por el punto P(x₀,y₀) y con vector director =(v_x,v_y), siempre que v_x≠0 y v_y≠0  viene dada por la expresión:

Ecuación general:

Consiste en multiplicar en cruz en la ecuación continua, y ordenar todos los términos en el mismo lado de la igualdad, obteniendo la siguiente expresión:

v_y·(x-x₀)=v_x·(y-y₀) operando obtendremos la ecuación general.

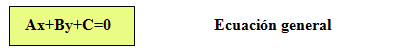
Podemos relacionar los coeficientes de la x y de la y con las coordenadas de un vector director de la recta sin más que identificar la ecuación general y la obtenida al multiplicar en cruz la continua:

A=v_y y B=-v_x  siendo el vector director entonces v=(-B,A)

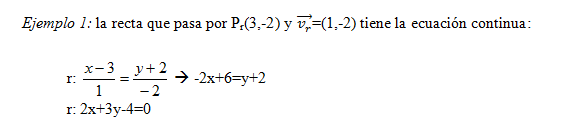
Nota: la ecuación continua también se puede obtener a partir de la ecuación punto pendiente (que veremos en el siguiente apartado).