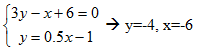Contenido
Altura
La altura de un triángulo es cada una de las rectas que pasa por el vértice del triángulo y que es perpendicular al lado opuesto del vértice.
Metodología para el cálculo de la altura:
- Calculamos la pendiente de la altura sabiendo que es perpendicular al lado opuesto
- Conocemos la pendiente y un punto de la recta (vértice), luego por la ecuación punto pendiente calculamos la recta pedida.
Ejemplo: dado el triangulo ABC con A(2,0), B(3,-1) y C(1,3), calcular la altura del vértice A.
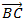=(-2,4) →m=4/(-2)=-2 . Luego la pendiente de la altura de A es la inversa con signo cambiado →m=0.5- La altura será entonces r: y-0=0.5(x-2) → r: y=0.5·x-1.
Ortocentro
El ortocentro de un triángulo es el punto donde se cortan las tres alturas. Para calcularlo basta con
1) calcular dos alturas
2) ver el punto de corte entre ambas.
Ejemplo: dado el triangulo ABC con A(2,0), B(3,-1) y C(1,3), calcular el ortocentro.
La altura del vértice A ya calculada → y=0.5·x-1.
La altura del vértice B: el vector 
=(-1,3) y su pendiente es m=-3, luego la pendiente de la altura es m=1/3 y pasa por el punto B(3,-1). Esta recta es r': (y+1)= (x-3) → r': 3y-x+6=0
El ortocentro es el punto de intersección de amabas rectas:
