Diagrama de árbol
En los dos apartados anteriores vimos sucesos compuestos, donde el resultado final sólo se llega a él por un único camino. Por ejemplo para sacar dos caras la primera moenda ha de ser cara y la segunda también tiene que ser cara. Muchas veces hay varios caminos para llegar al suceso final, sin salirnos de lanzar dos monedas podemos pensar el que salga una cara y una cruz, aquí hay dos caminos primera moneda cara y segunda cruz y al revés,
En este apartado veremos como resolver los sucesos compuestos donde al suceso final se llega de varias formas, estos problemas se solucionan por lo que se conoce como diagrama de árbol.
Se utiliza tanto cuando los sucesos son independientes como dependientes.
La probabilidad será igual a la suma de las probabilidades de los diferentes caminos que llegan a la solución final
Ejemplo: tenemos un clásico diagrama de árbol, en el cual hacemos el árbol de los posibles resultados de un experimento que consiste en lanzar una moneda (una cara perro y otra gato y un dado.
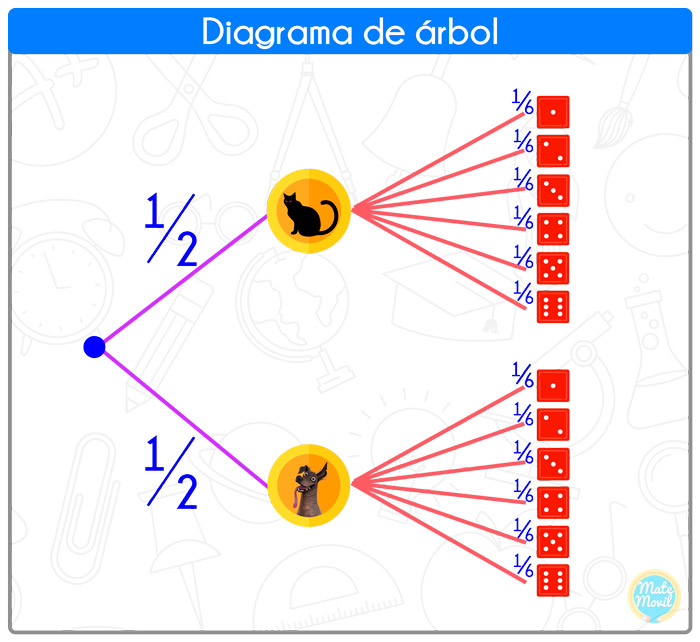
ara el cálculo de las probabilidades, usaremos un truco, si para calcular cierta probabilidad avanzamos hacia la derecha, entonces multiplicamos. Por otro lado, si para calcular cierta probabilidad avanzamos hacia abajo, entonces sumamos.

Si queremos calcular la probabilidad de que
1) Salga un gato y un número par: tenemos 6 caminos para llegar a gato y par: gato y 2, gato y 4, gato y 6
p(gato y 2)=1/2·1/6=1/12
p(gato y 4)=1/2·1/6=1/12
p(gato y 6)=1/2·1/6=1/12
p(gato y par)=p(gato y 2)+p(gato y 4)+p(gato y 6)=1/12+1/12+1/12=3/12=1/4






