En este apartado vamos a ver como se relaciona la probabilidad de los sucesos con la unión, la intersección y el suceso complementario.

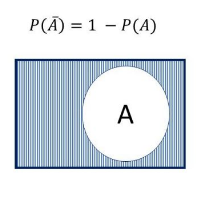
Suceso contrario: podemos relacionar las probabilidades de un suceso y la de su contrario. Se cumple así la siguiente relación: 

                                                                                   p(Ā)=1-p(A)

Esta propiedad puede ser muy útil, pues a veces es más fácil calcular la probabilidad del suceso contrario que la del suceso.

Ejemplo: Hallar la probabilidad de que al lanzar tres monedas se obtengan al menos una cara.

Es mucha más fácil si pensamos la probabilidad de que no salga ninguna cara, suceso contrario. Tenemos que hay 8 posibilidades (variación con repetición de 2 elementos de 3 en 3 → 2³) y sólo uno en el que salgan todas cruces

A="al menos una cara" → Ā="ninguna cara"={xxx}

p(A)=1-p(A)=1-1/8=7/8

Veamos el diagrama de Venn:

Probabilidad de la unión y la intersección: Si A y B son dos sucesos de un mismo experimento aleatorio, la probabilidad de la unión y de la intersección se relacionan de la siguiente forma:

Veamoslo gráficamente: 

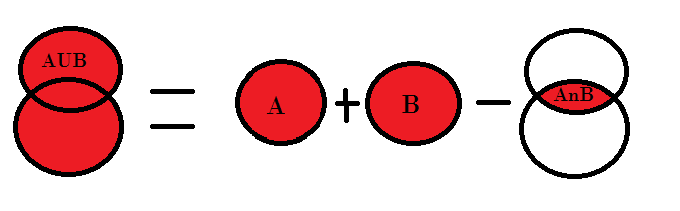
                                     p(A∪B)               =                     p(A)             +              p(B)          -            p(A∩B)

Nota: Si son sucesos incompatibles, sin sucesos en común (recordad que entonces p(A∩B)=0) se cumple que p(A∪B)=p(A)+p(B).

Ejemplo: en un quiosco de cada 10 personas que van a comprar se cumple que 5 compran un periódico, 3 una revista y 1 de ellos compra revista y periódico. Calcular la probabilidad de:

1. Que compren periódico, que compre revista
2. Que compren periódico y revista
3. Que compren periódico o revista

Solución:

1.     R="revista":  p(R)=3/10=0,3;          P="periódico": p(P)=5/10=0,5

2.     R∩P="revista y periódico":    p(R∩P)=1/10=0.1

3.      R∪P="revista o periódico" p(R∪P)=p(P)+p(R)-p(R∩P)=0,5+0,3-0,1=0,7