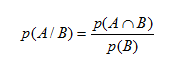La probabilidad condicionada es  la probabilidad de que ocurra un suceso A sabiendo que previamente ha ocurrido otro suceso B. La notación es la siguiente:

p("ocurra el suceso A sabiendo que antes ha ocurrido B")=p(A/B)

Al ocurrir el suceso B puede cambiar o no la probabilidad de que ocurra el suceso A. Veamos dos ejemplos, uno donde no cambia y otro en el que sí.

1. Sucesos independientes: la probabilidad de B no cambia la de A. Sacamos dos cartas de la baraja con reemplazamiento (sacamos la carta y la volvemos a meter y barajamos). ¿Que probabilidad hay de sacar un oro si antes hemos sacado una copa?

Llamaremos A="sacar oros 2ª carta" y B="sacar copa la 1ª carta"

Como hay reemplazamiento al suceso A, sacar oros, no le influye lo que hayamos sacado antes pues tenemos de nuevo la baraja completa: 

p(A/B)=p(A)=10/40=0,25

2. Sucesos dependientes: la probabilidad de B si cambia la de A. Sacamos dos cartas de la baraja sin reemplazamiento (sacamos la carta y la volvemos a meter y barajamos). ¿Que probabilidad hay de sacar un oro si antes hemos sacado una copa?

Llamaremos A="sacar oros 2ª carta" y B="sacar copa la 1ª carta"

Como no hay reemplazamiento al suceso A, sacar oros, si le influye lo que hayamos sacado antes pues ahora tenemos 39 cartas en la baraja y 10 oros:

p(A/B)=10/39=0,2564

Hay una fórmula que utilizaremos el próximo año que nos relaciona la dos probabilidades: