Para entender la gráfica de las funciones y=ax²+c tendremos que pensar que es una traslación en el eje OY de la función y=a·x² c unidades. De esta tal forma que el vértice situado en V(0,c). Si el valor de c es positivo (c<0) entonces el desplazamiento hacia arriba, siendo hacia abajo si por el contrario c es negativa (c<0)

La forma de la parábola sigue dependiendo del valor de a, tal que si a>0 es cóncava (U) y si a<0 es convexa.

Veamos algún ejemplo representándolas siempre con su función y=ax² asociada.

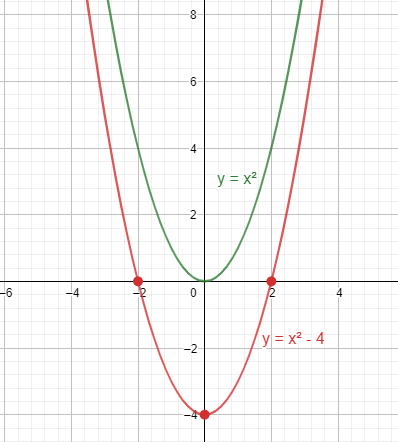
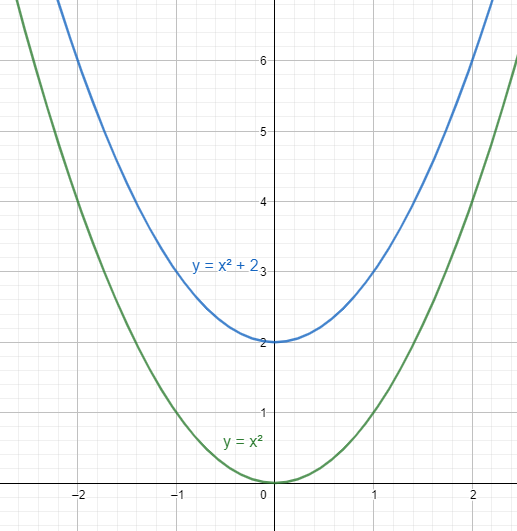
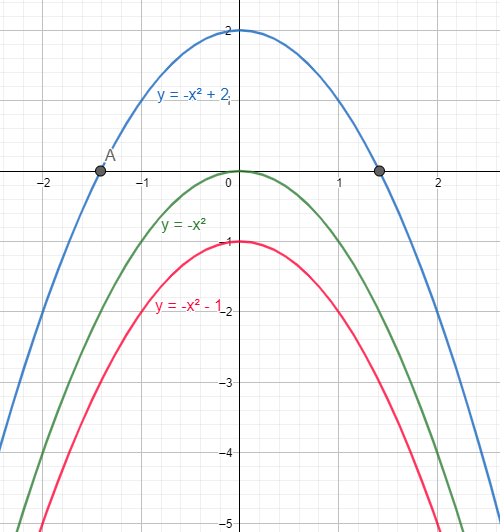
Cuando representemos gráficas de este tipo es importante ver el punto de corte con el eje OX, que como sabes es cuando y=0. Si te fijas en las gráficas de arriba solo cortan si c>0 y a<0 (cóncava con el vértice por encima del eje OX) o cuando c<0 y a>0 (convexa con el vértice debajo eje OX).

Veamos los pasos para representar la función con dos ejemplo y=f(x)=-x²-4 e y=g(x)=-x^2₊2

1. Miramos el valor de a y así sabremos su forma. Tanto en f(x) como en g(x) ambos a=-1<0  luego tiene forma ∩
2. Posición del vértice en V(0,c). En nuestros ejemplos V(0,-4) y V(0,2)
3. Puntos de corte con el eje OX: 
   1. -x²-4=0 → x²=-4 . No solución → no corta con el eje OX
   2. -x²+2=0 → x²=2 → x=±√2=±1,41   → dos puntos (-1.41,0) y (1.41,0)
4. Tabla de valores en torno al vértice:

   1. x	-2	-1	0	1	2
      y	-8	-5	-4	-5	-8

   2. x	-2	-1	0	1	2
      y	-8	-5	-4	-5	-8

5. Representar la curva