La traslación de las gráficas de las funciones y su efecto en su expresión analítica nos permite representar muchas funciones a partir de un patrón mucho más sencillo.

Dentro de las traslaciones distinguimos dos:

• Traslación horizontal
• Traslación vertical

Traslación horizontal:  Sea una función y=f(x), si trasladamos la gráfica x₀ unidades en eje OX entonces la expresión analítica de la función resulta de cambiar x por (x-x₀).

Ejemplo: f(x)=x³+x si lo trasladamos 2 unidades a la izquierda (x₀=-2)  obtendremos la sunción g(x)=f(x+2)=(x+2)³+(x+2)=x³+6x²+13x+10. Veamos el resultado gráficamente:

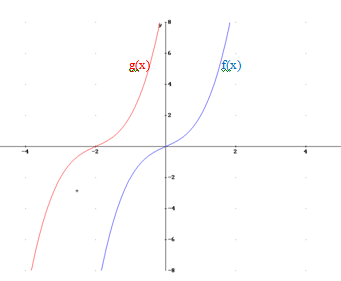
Gráfica de la función g(x) desplazada x₀=-2 (roja) respecto de f(x) (azul)   

Traslación vertical:   Sea una función y=f(x), si trasladamos la gráfica y₀ unidades en eje OY entonces la expresión analítica de la función resulta de cambiar y por (y-y₀) o lo que es lo mismo y=f(x)+y₀

Ejemplo: f(x)=x³+x si lo trasladamos 4 unidades hacia arriba (y₀=4)  obtendremos la función g(x)=x³+x+4.

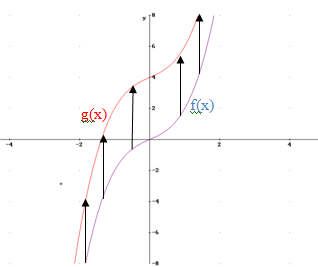
Gráfica de la función g(x) desplazada y₀=4 (roja) respecto de f(x) (azul)