Traslación de funciones
Funciones lineales
Funciones lineales
La expresión analítica de una recta es y=f(x)=mx+n. Se caracteriza por tener un crecimiento o decrecimiento constante. Un ejemplo claro es la posición de un móvil en el tiempo en el movimiento rectilíneo uniforme (s=s0+v·t, ejemplo s0=1m, v=2m/s à s(t)=1+2t).
Veamos el significado de m y n:
- m=pendiente de la recta, nos explica el crecimiento de la función. Si m>0 crece y si m<0 decrece, siendo la función contante si m=0. Se cumple así que:

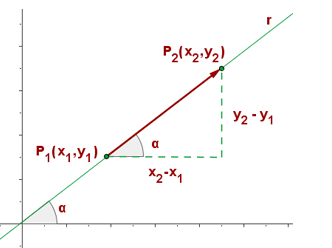
- n o b ordenada en el origen, es el punto de corte de la gráfica con el eje OY (es decir corta en el punto (0,n) o (0,b) )
m=\frac{\Delta x}{\Delta y}
Geogebra en las funciones lineales
En la siguiente página puedes modificar las barras de la pendiente, m, y la ordenada en el origen, b, y ver como se modifica la gráfica.
Es básico que entiendas como influye cada parámetro de la función en la gráfica.
Para que comprendas el significado te propongo 3 gráficas:
- y=x-3 (m=1 y b=-3)
- y=-4 (m=0 y b=-4)
- y=-x+2 (m=-1 y b=2)
Representar funciones lineales
Ejercicio, relacionar gráfica y ecuación
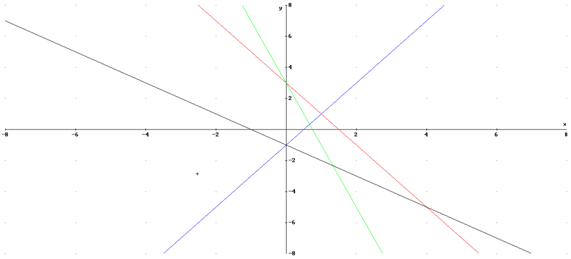
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0