Como obtener la ecuación de la función lineal
Vamos a ver como obtener la ecuación de la función lineal, y=mx+n según distintas opciones:
- Conocido dos puntos A(x1,y1) y B(x2,y2). Podemos hacerlo de dos maneras
- Mediante resolución de un sistema de ecuaciones: los dos puntos A y B son de la recta y por tanto cumple la ecuación y=mx+n. Sustituyendo los valores x e y de la ecuación por x1 e y1 obtenemos una ecuación con dos incógnitas, m y n. Si hacemos lo mimos con x2,y2 tendremos otra ecuación y por tanto un sistema (facilmente resoluble por reducción, restando las ecauciones, reducción)
- Mediante la ecuación punto pendiente: es una ecuación que se utiliza si conocemos la pendiente, m, y un punto A(x1,y1). La ecuación es y=y1+m(x-x1). Operando obtendremos la ecuación.
- Conocido un punto A(x1,y1) y una recta y=mx+n de la que es paralela. La nueva recta tiene la misma pendiente que la que es paralela (la pendiente marca el crecimiento, que es el mismo), por lo que utilizando la ecuación punto pendiente, y=y1+m(x-x1), obtendremos la ecuación.
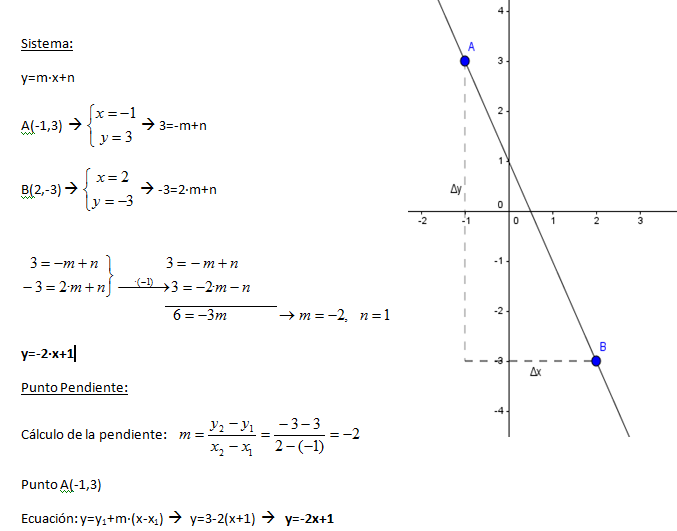
Ejemplo 1: Calcular la ecuación de una recta que pasa por A(-1,3) y B(2,-3).
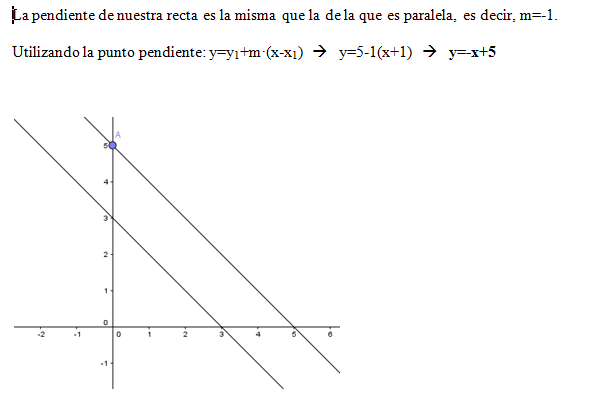
Ejemplo 2: Calcular la ecuación de la recta paralela a y=-x+3 que pasa por A(0,5)
La pendiente de nuestra recta es la misma que la de la que es paralela, es decir, m=-1.
Utlizando la punto pendiente: y