Para entender la gráfica de la función y=ax²+bx+c basta con expresar la función de la forma  y=y₀+a(x-x₀)² la gráfica será entonces igual que el de la parábola y =ax² pero desplazada x₀ en el eje OX e y₀ en el eje OY. De esta forma el vértice está en V(x₀,y₀). En la práctica lo más importante es calcular el vértice, que como veremos es muy fácil, y los valores de la función a ambos lado de este. 

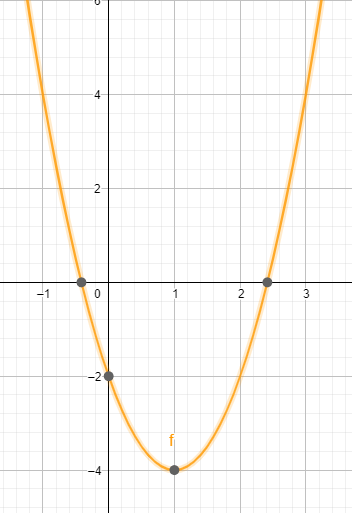
Pasos para representar, utilizaremos la función y=2x²-4x-2

1. Nos fijamos en el valor de a, si a>0 será cóncava (∪) siendo convexa si a<0 (∩). En nuestro ejemplo a=2> concava
2. Calculamos el vértice V(x₀,y₀) siendo x₀=-b/(2a) e y₀ lo optendremos sustituyendo el valor de x₀ en la función. En nuestro ejemplo x₀=-(-4)/2·2=1 e y₀=2·1²-4·1-2=-4, luego V(1,-4)
3. Puntos de corte con eje OX (y=0): resulta de resolver la ecuación de segundo grado x²+bx+c=0. Sino tiene solución no tendrá punto de corte con el eje OX. En nuestro ejemplo 2x²-4x-2=0 → x=1±√2, luego los puntos son  (1+√2, 0)=(2.41,0) y (1-√2, 0)=(-0.69,0)
4. Representar la gráfica dando valores a la izquierda y derecha del vértice (de x=x₀). En nuestro ejemplo 

   X	-1	0	1	2	3
   y	4	-2	-4	-2	4