Contenido
Definición: dos figuras se dicen que son semejantes si tienen misma forma de tal manera que se cumple:
- Los ángulos correspondientes son todos iguales
- Los lados son todos proporcionales entre si. La razón de proporcionalidad (cociente entre lados correspondientes) se llama razón de semejanza
Ejemplo:
- todos los cuadrados son semejantes (ángulos iguales y lados proporcionales)
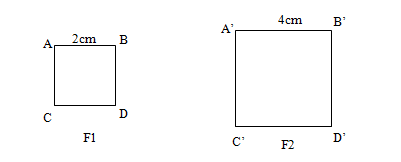
Luego la figura F1 es semejante a F2 con razón de semejanza de k=4/2=2
- Todos los circunferencias son semejantes
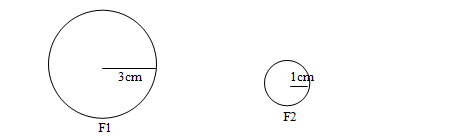
Luego la figura F1 es semejante a F2 con razón de semejanza de k=3/1=3
- Veamos un ejemplo de dos figuras arbitrarias semejantes:
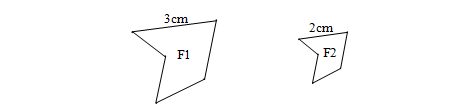
La figura F1 es semejante a F2 con razón de semejanza k=3/2=1,5
En la vida corriente las figuras semejantes que se utilizan son por ejemplo los planos (en 2 dimensiones) o las maquetas (en 3 dimensiones).
Definición de escala: el concepto de escala es equivalente al de razón de semejanza, es la razón métrica entre un plano o maqueta y aquello a lo que representa.
La notación usual en los mapas es la siguiente 1:1000 que significa que 1cm en el mapa es en realidad 1000cm=10m. Es equivalente a una razón de semejanza k=1000.
Formas de construir figuras semejantes: hay varias formas veamos a partir de un punto fijo (foco):
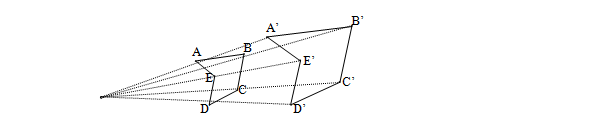
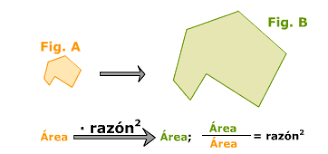
Importante: los lados y el perímetro de figuras semejantes se relacionan entre sí a partir de la constante de proporcionalidad k. En cambio el área que tiene dimensión 2 se relaciona con k2. Veamos algún ejemplo.
Ejercicio resuelto: calcular los lados que faltan
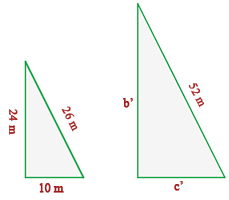
Calculemos el valor de la constante: k=52/26=2
c'=10·k=10·2=20
b'=24·k=24·=48
Si pensamos en el área:
el triángulo pequeño tiene un área=b·h/2=10·24/2=120
el triángulo grande tiene un área=b·h/2=20·48/2=480
Como ves la relación entre áreas es a partir de k2 : 480=22·120