En muchas situaciones se plantean problemas de optimización, es decir hacer que una función sea máxima o mínima para unas premisas impuestas.

Los casos de optimización que trabajaremos es cuando la función depende de una sola variable. Pasos a seguir para optimizar:

1. Expresar la función que deseamos optimizar en función todas variables.
2. Si la función tiene más de una variable relacionar las variables con los datos del problema y obtener una función de una sola variable.
3. Derivar la función, igualarla a cero y así obtener los puntos relativos
4. Comprobar, mediante la segunda derivada, si estos puntos son máximos o mínimos.

Veamos un ejemplo: Se quiere construir botes de enlatar de forma cilíndrica de 10 litros de capacidad. Calcular las dimensiones para que el gasto sea mínimo

El cilindro tiene dos variables, la altura que llamaremos y, y el radio que llamaremos x. Veamos el dibujo:

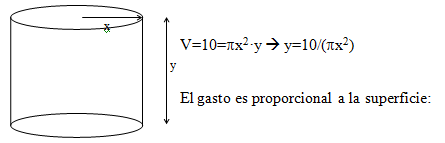
La función a optimizar es el gasto, o de forma equivalente la superficie:

superficie=f(x,y)=2·Abase+Alateral=2·π·x²+2·π·x·y  (queremos que sea mínimo)

Para que la función dependa solo de una variable tenemos que buscar una ligadura, es decir una relación entre la x y la y. En nuestro caso es el volumen de 10l=10dm³. V=Abase·h, que en función de x e y :  10=π·x²·y.

Por sencillez despejamos la y, de forma que y=10/(π·x²). Introduciendo este valor de y en función de x en la forma de superfice tendremos que sólo va a depender de x:    f(x)=2·π·x²+20/x. 

Para ver el valor mínimo o máximo tendremos que derivar e igualar a cero: f'(x)=4·π·x-20/x²=0. Poniendo común denominador tendremos la ecuación equivalente 4·π·x³=20 → 

Para ver si este valor de x genera un máximo o un mínimo tendremos dos opciones, viendo la monotonía o la segunda derivada. Puedes elegir el método que prefieras.:

Metodo 1 para ver si es máximo o mínimo: Monotonía

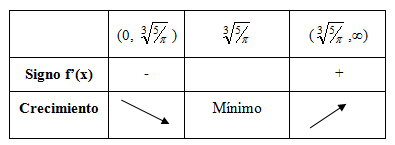
Metodo 2 para ver si es máximo o mínimo: segunda derivada