Veamos las definiciones de los dos tipos de curvaturas posibles en una función:

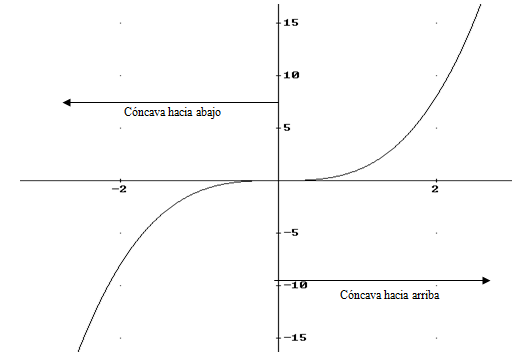
Definición 1: Una función es cóncava hacia las y positivas o cóncava hacia arriba en un punto P(x₀,y₀), si la recta tangente en este punto está por debajo de los puntos próximos a P. Gráficamente tiene forma de ∪

Definición 2: Una función es cóncava hacia las y negativas o cóncava hacia abajo en un punto P(x₀,y₀), si la recta tangente en este punto está por encima de los puntos próximos a P. Gráficamente tiene forma de ∩.

Podemos saber si una función es cóncava hacia arriba o hacia abajo a partir de la segunda derivada:

• Si f’’(x₀)>0, entonces f(x) es cóncava hacia arriba en el punto (x₀,f(x₀)). (Recordar la curvatura de y=f(x)=x² y como f’’(x)=2>0)
• Si f’’(x₀)<0, entonces f(x) es cóncava hacia abajo en el punto (x₀,f(x₀)). (Recordar la curvatura de y=f(x)=-x² y como f’’(x)=-2<0)

Ejemplo: y=f(x)=x³  f’’(x)=6x, si x>0 cóncava hacia arriba y si x<0 hacia abajo

Puntos de Inflexión

Uno de los puntos más importantes a la hora de representar una función son los puntos de inflexión; veamos que es un punto de inflexión:

Definición: Se dice que f(x) tiene punto de inflexión en (x₀,f(x₀)) si en ese punto cambia la curvatura de la función, es decir pasa de ser cóncava hacia arriba a cóncava hacia abajo o al revés. En este punto la recta tangente a la función corta a la función.

Vamos a ver la relación entre los puntos de inflexión y las derivadas de la función, en el siguiente teorema:

Si f(x) cumple en x₀ que la segunda derivada es nula (f’’(x₀)=0) y además la tercera derivada es distinta de cero (f’’’(x₀)≠0), entonces la función f(x) tiene un punto de inflexión en (x₀,f(x₀)).

En el caso de que tanto f’’(x₀)=0 como f’’’(x₀)=0, tendremos que recurrir a las derivadas de orden superior, y ver el orden de la primera no nula en x₀ (lo veremos el próximo año).

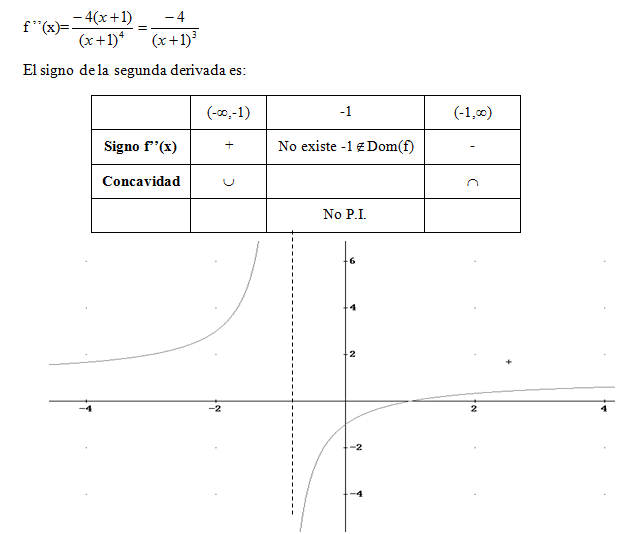
 Ejemplo:Estudia el crecimiento, puntos relativos, la curvatura y los puntos de inflexión de la función f(x)=(x-1)/(x+1)

Primero estudiemos el dominio Dom(f)=R-{-1}

Vemos que siempre es positiva para todo valor de x que pertenezca al dominio:

Calculemos ahora la curvatura y los puntos de inflexión