En el tema anterior relacionamos las derivadas con la pendiente de las rectas tangentes a la gráfica descrita por la función, es decir, f ’(x₀) es la pendiente de la recta tangente a la gráfica f(x) en x=x₀.

Vamos a relacionar el signo de m=f’(x₀) con el crecimiento o decrecimiento de la función; para esto nos valemos del siguiente ejemplo:

y=f(x)=x³-12x+5    →    f’(x)=3x²-12=3·(x-2)·(x+2)

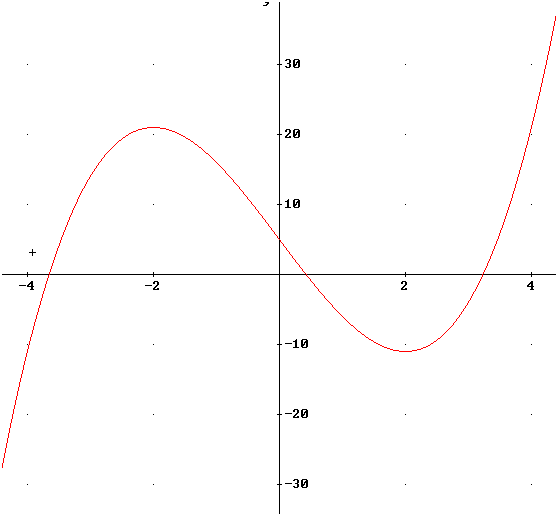
Gráfica de f(x)

Podemos ver el signo de la derivada para determinar a partir de este el crecimiento, decrecimiento o puntos máximos o mínimos (puntos relativos) de la función. Para ver el signo de la derivada lo que hacemos es ver cuando f'(x)=0, es decir sus raíces, y miramos el signo en los intervalos entre dichas raíces ( hay que incluir las asíntotas si las tuviera).

En nuestro ejemplo:

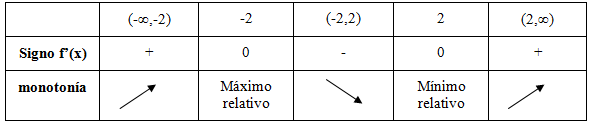
Claramente vemos que cuando f ’(x₀)>0 la recta tangente es creciente, pues la pendiente es positiva, y por lo tanto f(x) es creciente en x_0. De igual forma si f ’(x₀)<0 la recta tangente es decreciente, pues su pendiente es negativa, y por lo tanto f(x) es decreciente en x₀

Conclusión:

1. Si f’(x₀)>0 la función f(x) es estrictamente creciente en x₀
2. Si f’(x₀)<0 la función f(x) es estrictamente decreciente en x₀