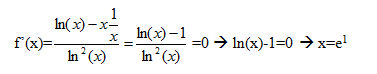Extremos relativos
Antes de relacionar los extremos relativos con la derivada definámoslos.
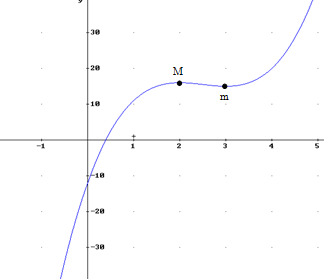
Definición: Extremo relativo de una función f(x) es todo punto x0 tal que, para todo entorno del punto E(x0,r), se cumple que la función en este intervalo crece y decrece. Según crezca antes o después de x0, distinguimos dos tipos de extremos relativos:
a) Máximo relativo en x0: la función crece hasta x0 y decrece a partir de x0.
b) Mínimo relativo en x0: la función decrece hasta x0 y crece a partir de x0.
Está claro que si x0 es un extremo relativo de f(x), en este punto la gráfica ni crece ni decrece, luego una condición necesaria es que f’(x0)=0, así la pendiente de la recta tangente es m=0, siendo por tanto paralelo al eje x. Pero está no es la única condición. Es necesario, que además, se cumpla una segunda condición que además nos permite discernir si es máximo o mínimo relativo:
- Sea x0 un punto de una función en el que se cumple
- f ’(x0)=0
- f ’’(x0)<0
entonces (x0,f(x0)) es máximo relativo
- Sea x0 un punto de una función en el que se cumple
- f ’(x0)=0
- f ’’(x0)>0
entonces (x0,f(x0)) es mínimo relativo
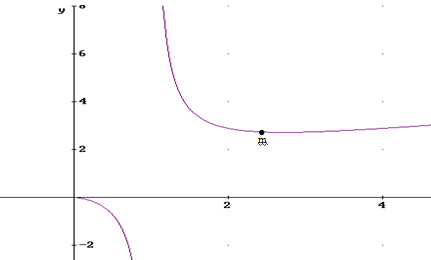
En la práctica, si se cumple que f ’(x0)=0 y viendo el crecimiento de la función antes y después del punto podemos ver si es punto relativo y si es máximo o mínimo.
En el caso de que f ’(x0)=0 pero también f ’’(x0)=0, no podemos asegurar que este punto sea extremo relativo y hay que estudiar las derivadas de orden superior (se verá en el próximo curso).