Estudia la distribución de los valores de la serie, analizando si estos se encuentran más o menos concentrados, o más o menos dispersos.

Existen diversas medidas de dispersión, entre las más utilizadas podemos destacar las siguientes:

• Rango o recorrido
• Varianza
• Desviación típica
• Coeficiente de variación.

 Rango o recorrido: mide la amplitud de los valores de la muestra y se calcula por diferencia entre el valor más elevado y el más bajo. Se representa por R

          R=x_max-x_min

  En nuestros ejemplos: ejemplo 1à R=3-0=3, ejemplo 2 à R=91-60=31

Varianza: es la media aritmética de los cuadrados de las desviaciones de todos los datos o marcas de clase respecto a la media. Se representa por σ² o Var(x):

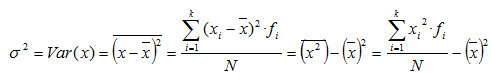
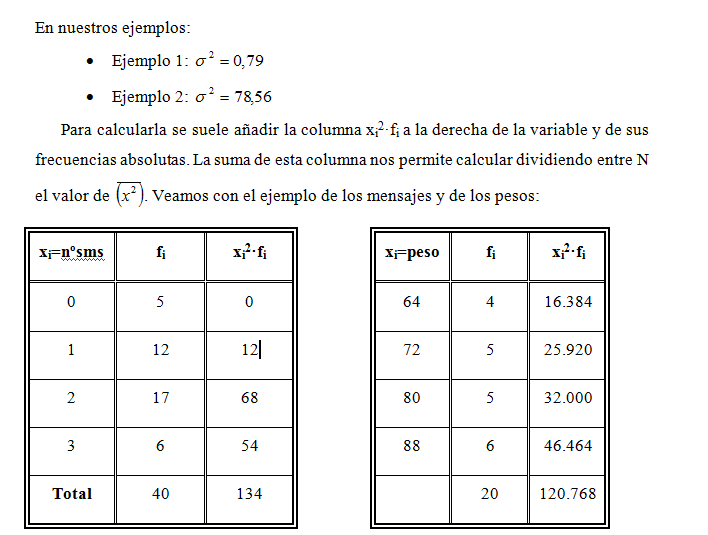
La varianza no tiene las mismas unidades que x (si x es metros s² será metros cuadrados). Es por eso que se utiliza más la desviación típica.

Desviación típica: es la raíz cuadrada de la varianza. Tiene mismas dimensiones que la variable estadística en estudio. Se denota por s

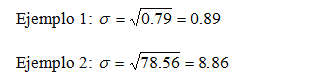
En la medida en que los parámetros de dispersión tomen valores más o menos grandes esto nos indicara el grado de dispersión o alejamiento de los datos respecto de la media. En el caso trivial que todos los datos centrados en un mismo valor todos estos parámetros valdrían cero.

Coeficiente de variación: las medidas de dispersión estudiadas hasta ahora se expresan en la misma medida que la variable estadística, designando medidas de dispersión absolutas respecto de la media. Esto presenta los siguientes problemas:

• No podemos comparar distribuciones de distinta naturaleza (peso y altura) o incluso de la misma naturaleza expresadas en distintas unidades.
• No es relativa al valor de la media: la variación de 100€ respecto de 1.000€ es mucho más significativa que la de los mismos 100€ respecto a 1.000.000€.

Estos problemas se resuelven con el coeficiente de variación, que es el cociente entre la desviación típica y la media, siendo por tanto adimensional.