Estos parámetros nos indican en torno a que puntos se encuentran los valores de la variable cuantitativa en estudio. Es la forma de representar un conjunto de datos mediante un solo valor, tratando de resumir o sintetizar la distribución de frecuencias. Los parámetros más importantes son:

• Media (aritmética y geométrica)
• Moda
• Mediana

1. Media: es el valor medio ponderado de la serie de datos. Se pueden calcular diversos tipos de media, siendo las más utilizadas:

Media aritmética: se calcula multiplicando cada valor por el número de veces que se repite. La suma de todos estos productos se divide por el total de datos de la muestra. La media aritmética es el parámetro de centralización más importante y más usada. La media aritmética de un conjunto de datos x_i se representa por . Su cálculo se realiza de la siguiente forma:

1. Datos sin frecuencia:

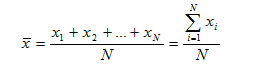
2. Si tenemos k datos distintos con sus frecuencias (tabla de frecuencias):

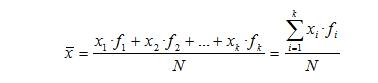
3. Con datos ponderados: es cuando queremos dar más “peso” a algunos datos que otro. Si llamamos l_i al peso en tanto por cien la media ponderada es:

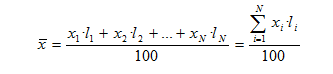
Ejemplo: nota media ponderada de 3 exámenes, el primero pondera 30% el segundo 30% y el tercero 40% si x₁, x₂, x₃ las notas de los tres exámenes:

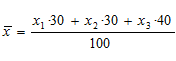
Veamos la media en los dos ejemplos cuantitativos que desarrollamos en el tema:

Ejemplo 1:

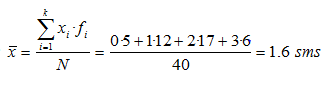
Ejemplo 2: en las variables continuas se suele aproximar utilizando las marcas de clase en vez de los verdaderos valores, a fin de simplificar los cálculos.

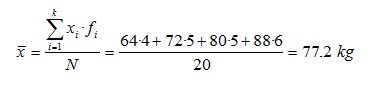
Para el cálculo de la media muchas veces se realiza una tabla con las siguientes tres columnas: los valores x_i, las frecuencias absolutas f_i, el producto x_i·f_i. En las celdas inferiores se hace la suma de todos los productos x_i·f_i, siendo la media por tanto esta suma entre N:

xi=nºsms	fi	xi·fi		xi=peso	fi	xi·fi
0	5	0		64	4	256
1	12	12		72	5	360
2	17	34		80	5	400
3	6	18		88	6	528
Total	40	64			20	1544

                                                        

Media geométrica: se eleva cada valor al número de veces que se ha repetido. Se multiplican todo estos resultados y al producto final se le calcula la raíz "N" (siendo "N" el total de datos de la muestra).

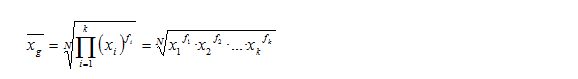
La media geométrica se suele utilizar en series de datos como tipos de interés anuales, inflación, etc., donde el valor de cada año tiene un efecto multiplicativo sobre el de los años anteriores. En todo caso, la media aritmética es la medida de posición central más utilizada.

Las medias (tanto en el caso de la media aritmética como geométrica) presenta el problema de que su valor  se puede ver muy influido por valores extremos, que se aparten en exceso del resto de la serie. Estos valores anómalos podrían condicionar en gran medida el valor de la media, perdiendo ésta representatividad

2. Moda (M₀): es el valor que más se repite en la muestra.

Calculo en las variables cuantitativas discretas (también cualitativas): para calcularlo basta con buscar el valor de la variable que presenta más frecuencia. Puede ocurrir que la moda no sea única, es decir, la distribución tenga 2, 3,… modas, recibiendo el nombre de bimodales, trimodales, etc.

En nuestro ejemplo 1 la moda es 2 sms, pues es el de mayor frecuencia absoluta (17)

Calculo en la variable continua: se puede hacer de forma aproximada con las marcas de clase, aunque si se quiere ser más preciso se puede obtener mediante la expresión:

siendo:

• L_i el límite inferior de la clase modal
• c la amplitud del intervalo modal
•  las frecuencias absolutas de la clase modal, la anterior y la siguiente.

Este valor M₀ es la intersección de las rectas que unen los extremos de la clase modal con los extremos más próximos de las clases anterior y siguiente:

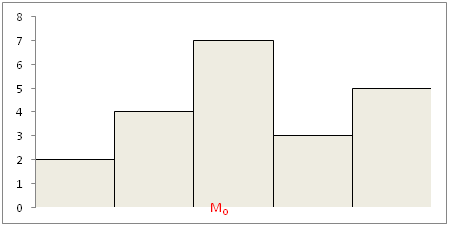
En nuestro ejemplo 2, el valor aproximado de la moda es el intervalo [84,92], pues es el que tiene mayor frecuencia absoluta (6). Si queremos calcular M₀ de forma exacta usemos la formula (L_i=84, e=8, f_i=6, f_i-1=5, f_i+1=0) → M₀=85,14.

3. Mediana (M_e): ordenados los N elementos en orden creciente es el que ocupa la posición intermedia, siendo el 50% de los datos menores o iguales que M_e y el restante 50% mayores o iguales que M_e.

Calculo para variable cuantitativa discreta: es el primer valor que supera el 50% en porcentaje acumulado (o N/2 en frecuencia absoluta acumulada). Puede ocurrir cuando N es par que un dato tenga frecuencia acumulada de 50%, en este caso la mediana se considera la media entre el dato con dicha frecuencia acumulada y el siguiente dato.  En nuestro ejemplo 1 la mediana es 2 mensajes.

Calculo para variable cuantitativa continua: de forma aproximada se hace igual que para la variable discreta usándolas marcas de clase. Si se quiere ser más exacto se debe buscar el valor de la recta frecuencia acumulada que valga N/2. La formula es la siguiente:

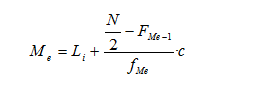
siendo:

• L_i el límite inferior de la clase mediana
• c la amplitud del intervalo mediana
• f_Me la frecuencia absolutas de la clase modal.
• N el número total de datos.
• F_Me-1  la frecuencia absoluta acumulad hasta llegar a la mediana sin incluirla.

La formula se puede obtener gráficamente por semejanza de triángulos ABC y APQ:

 

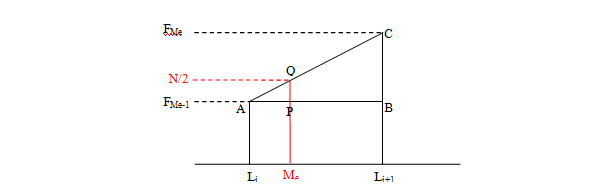
En nuestro ejemplo 2, la mediana aproximada es M_e=80, y si la calculamos de forma exacta: