Como vemos en los tres ejemplos del tema los datos tal como están presentados no nos dan gran información, es por esto que la forma usual y útil de presentar los datos es en forma de tabla estadística, una vez realizado el recuento. 

El recuento en Estadística se realiza de la forma siguiente:

1. En una columna (fila) se ponen los distintos valores que toma la variable, x_i (agrupados en intervalos si son continuos).
2. En la siguiente columna (fila) se pone la frecuencia absoluta, f_i, de cada valor de la variable: número de veces que aparece dicho valor.
3. Generalmente se añaden otros parámetros estadísticos en las sucesivas columnas (filas) como la frecuencia relativa, frecuencias acumuladas y tanto por cien.

La frecuencia relativa (h_i): es el cociente entre la frecuencia absoluta y el número total de elementos de la encuesta, N. Se puede entender como el tanto por uno

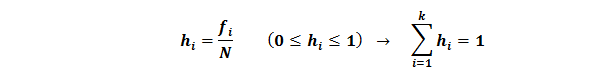
Tanto por cien (p_i): como su nombre indica nos indica el porcentaje relativo a 100 de la característica respecto del total:

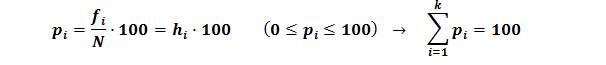
La frecuencia absoluta acumulada (F_i): es la suma de todas las frecuencias absolutas hasta la i-esima (incluida), es decir

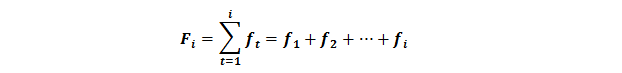
La frecuencia relativa acumulada (H_i): es la suma de todas las frecuencias relativas hasta la i-esima (incluida), es decir

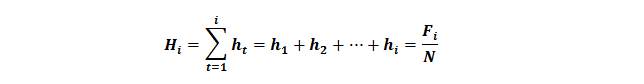
El porcentaje acumulado (P_i): es la suma de todos los porcentajes hasta el i-esimo (incluido), es decir

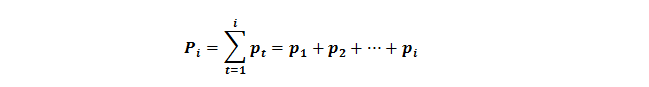
Para calcular las frecuencias acumuladas utilizar la relación entre dos frecuencias acumuladas sucesivas: F_i+1=F_i+f_i+1 , H_i+1=H_i+h_i+1, P_i+1=P_i+p_i+1

Veamos en los ejemplos anteriores como quedaría la tabla de frecuencias:

Ejemplo 1. Variable cuantitativa discreta: la siguiente lista representa el número de mensajes recibidos en los teléfonos móviles de 40 personas en un día:

3, 2, 1, 2, 0, 2, 1, 3, 2, 1, 1, 0, 2, 2, 1, 1, 3, 2, 1, 3, 2, 3, 1, 1, 0, 2, 2, 1, 2, 2, 0, 2,2,1, 2, 3, 2, 0, 1, 2.  

Ejemplo 3. Variable cualitativa: colores de los coches del claustro de profesores (20 profesores): rojo, rojo, blanco, negro, azul, gris, gris, negro, verde, amarillo, blanco, rojo, gris, amarillo, azul, azul, verde, amarillo, blanco, gris.

En las variables cualitativas no tiene sentido hablar de las frecuencias acumuladas, ya que las características no son números y por tanto no se pueden ordenar

Ejemplo 2. Variable cualitativa continua: Pesos de 20 asistentes a una reunión: 72, 63, 88, 91, 65,77, 81, 60, 84, 70, 75, 73, 78, 88, 64, 69, 86, 77, 90, 80.

Hemos dejado esta para el final, pues hay que elaborar los intervalos. Para hacerlos debemos conocer el rango, que es la diferencia máxima entre dos valores, y el número de intervalos en los que deseamos clasificar la variable.

Rango=R=x_max-x_min=91-60=31. Y vamos a agruparlos en 4 intervalos. Si queremos hacerlo exacto el numero rango de cada intervalos será 31/4=7,75, aunque es más lógico ampliar el rango con el fin de que este número sea exacto. En nuestro caso ampliaremos el rango a 32, con lo que cada intervalo tendrá un recorrido de 32/4=8. Al ampliar dicho rango en 1 tendremos que comenzar 1 unidad antes o acabar 1 después. Hagamos lo segundo (puede hacerse una u otra indistintamente)

Las marcas de clase son los puntos medios de los intervalos.

Nota: las amplitudes de las clases no tienen por qué ser iguales, esto lo tendremos muy en cuenta cuando representamos la gráfica del histograma.