Contenido
El teorema de Euler relaciona el número de caras (C), vértices (V) y aristas (A) de todo poliedro convexo (sin orificios, ni entrantes), cumpliéndose:
C+V=A+2
Puedes ver la diferencia entre poliedro convexo (cumple Euler) y no convexo o cóncavo en el siguiente ejemplo:

Vamos a comprobar el teorema de Euler en los tres poliedro convexos del dibujo anterior:
1. 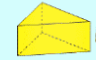 C=5, V=6, A=9 ⇒ C+V=A+2 ⇒ 5+6=9+2
C=5, V=6, A=9 ⇒ C+V=A+2 ⇒ 5+6=9+2
2. 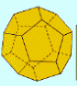 C=12, V=20, A=30 ⇒ C+V=A+2 ⇒ 12+20=30+2
C=12, V=20, A=30 ⇒ C+V=A+2 ⇒ 12+20=30+2
3. 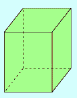 C=6, V=8, A=12 ⇒ C+V=A+2 ⇒ 6+8=12+2
C=6, V=8, A=12 ⇒ C+V=A+2 ⇒ 6+8=12+2