
Figura 1
2. Experimento realizado en el Instituto
Eratóstenes, nacido en Cirene en el año 284 antes de Jesucristo, y muerto en Alejandría a los 92 años, fue el primer científico de la historia de la Humanidad en medir con bastante precisión, la circunferencia de nuestro planeta.
Eratóstenes midió la circunferencia terrestre por primera vez con una gran exactitud, en una época en la que muy poca gente pensaba que el mundo no era plano como una mesa.
Pero, ¿cómo lo hizo?. ¿En qué se basó para hacer la medida del radio de la esfera terrestre?

Pues, pensó, sencillamente, que dos estacas clavadas verticalmente en el suelo, a una distancia de varios kilómetros, sobre un mismo meridiano, darían sombras distintas a una misma hora en virtud de la curvatura de la superficie del planeta.
Los ángulos que forman los rayos de sol con la dirección de la estaca son:
a1=arctg(s/d) y a2=arctg(s'/d)
Siendo s y s’ la sombra de cada estaca sobre la línea meridiana en cada lugar. La longitud de la estaca es d en ambos casos.
Si observamos ahora la figura 2 y nos fijamos en el triángulo que se forma, con ángulos a ,a1 y 180-a2
donde a es el ángulo del arco de meridiano comprendido entre las posiciones que ocupan ambas estacas, y a1 y a2 son los ángulos que forman los rayos solares con la dirección de las estacas, vemos que, al sumar 180º los tres ángulos del triángulo es:
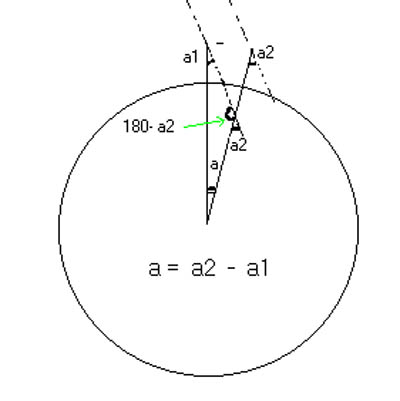
Conocido el ángulo a, y la longitud L del arco de meridiano
entre ambos puntos de colocación de las estacas, será posible, mediante una
sencilla regla de tres, encontrar la longitud total, X, de la circunferencia
del planeta:
y, de aquí, el radio medio de la Tierra:
Si una de las dos estacas, en un determinado momento diera sobre la línea meridiana sombra nula, es decir, si en una de las estacas fuera cero el ángulo que forma la dirección de los rayos solares con la estaca, o, dicho de otra manera, si en uno de los dos lugares los rayos solares inciden perpendicularmente, entonces, se tendría que:
a1 = 0, por lo cual a = a2 – 0 = a2, es decir, el ángulo, a, que corresponde al arco de meridiano terrestre comprendido entre ambas posiciones de las estacas, es, precisamente el ángulo, a2, que formarían los rayos solares con la segunda estaca sobre la línea meridiana.
Este último hecho fue lo que utilizó Eratóstenes para hacer su medición.
Eratóstenes, que estaba en Alejandría, recordó que en un cierto día del año, en el solsticio de verano, los rayos solares caían verticalmente en la ciudad de Siena, situada en el mismo meridiano que Alejandría, pues recordaba que el sol se reflejaba en lo mas profundo de los pozos, a la hora del mediodía. Entonces, pensó que si media ese día en la ciudad de Alejandría, a la misma hora, el ángulo, a2, que los rayos solares formaban con la vertical, midiendo la sombra que sobre la línea meridiana formaba la estaca, conocería el ángulo del arco de meridiano entre Alejandría y Siena.
Eratóstenes midió la sombra sobre la línea meridiana producida por una estaca vertical en Alejandría, y conociendo la longitud de la estaca halló ese ángulo a la hora antedicha: resultó que el ángulo era de 7 grados (a2 = 7º). Ya sabia el ángulo del arco de meridiano entre Alejandría y Siena. Ahora faltaba conocer la distancia, a lo largo del meridiano, entre ambas ciudades, es decir, la longitud del arco L. Para ello Eratóstenes pagó a un hombre que hizo, a pié, tal medición. Eran, usando la medida usual en la época y en la zona, unos 4900 estadios, que equivaldría hoy ( a unos 6’125 estadios por kilómetro) a unos 800 kms.
Con estos datos ya es inmediato el cálculo:
Longitud de la circunferencia terrestre:
Radio medio del planeta:
Experimento realizado en el Instituto
Todo empezó con a partir de la llamada desde la WEB de
Astronomía 2009 a los institutos españoles en repetir el experimento de Erastótenes, con una salvedad esta vez no había que caminar y contar los pasos entre los distintos institutos...para calcular las distancias puedes usar el visor sigpac.El caso es que desde más de 800 instituto, nos disponemos al cálculo de la altura solar (ángulo que forma el sol con el suelo horizontal) en el mismo instante solar (el Sol ocupe en todos ellos la misma posición). Pero surge el problema de que en cada instituto situado en distinto mismo meridiano... Esto implica que la hora solar es distinta en cada instituto. Tenemos que ponernos de acuerdo en la misma hora solar; la más sencilla de conocer es el MEDIODIA SOLAR, punto en el que el Sol situado en el punto más alto, y por tanto cuando la sombra del gnomon es la menor.
El experimento se realizó el día 26 de marzo, antes del cambio de hora de Verano (29 de Marzo), por lo que el medio día solar en el meridiano de Greenwich (Castellón) era en torno a las 13:00. Como Saldaña situada en la longitud 4,44 W el Sol "tardará en llegar" a nuestro instituto unos 18 minutos (15°=1 hora). Así que en torno a las 13:20 sería el medio día solar en Saldaña, instante en el que tendremos que medir la sombra de nuestro gnomon (un recogedor) para así calcular la altura del Sol.
Los alumnos de 4º ESO, ayudados de los de 3º ESO, 1º Bachillerato y 1º ESO realizaron medidas de la sombra del cogedor, nuestro gnomon, desde las 12:56 hasta las 13:51, rango horario donde se encuentra el Mediodía solar de Saldaña para ese día. La sombra que se produce es una parábola:
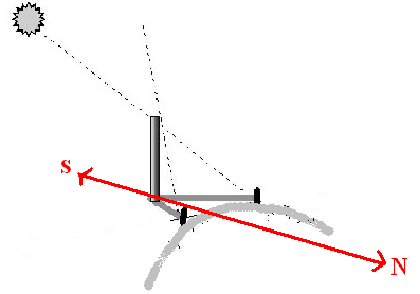
El vértice de la parábola es el punto con menor sombra del gnomon, es decir cuando el Sol situado en el punto más alto, ¡¡hemos encontrado el Mediodía Solar!!. Además con esta experiencia conocemos:
1. La recta que nos indica el Norte y el Sur (recta que pasa por el pie del gnomon y el vértice de la parábola)
2. El mediodía solar de Saldaña para el día 26 de Marzo.
3. Midiendo la sombra del gnomon a esta hora y el propio gnomon calculamos la altura solar, que necesitamos para calcular el radio de la Tierra.
Los datos obtenidos son los siguientes:
| Hora | Sombra(cm) | Altura solar |
| 12:56 | 86 | 49,6 |
| 13:01 | 85 | 49,9 |
| 13:06 | 84,7 | 50,0 |
| 13:11 | 84,5 | 50,1 |
| 13:16 | 84,3 | 50,1 |
| 13:21 | 84 | 50,3 |
| 13:26 | 84,1 | 50,2 |
| 13:31 | 84,5 | 50,1 |
| 13:36 | 84,7 | 50,0 |
| 13:41 | 85,3 | 49,8 |
| 13:46 | 86,2 | 49,5 |
| 13:51 | 86,5 | 49,4 |
| Tamaño gnomon | 101 |
Vemos que el mediodía solar está entre las 13:16 y las 13:26, cuando la sombra es la menor. La altura solar en Saldaña el día 26de Marzo al mediodía será próxima a 50°. Para calcular el vértice utilizamos la herramienta de Excel de representación lineal y del cálculo de la línea de tendencia, obteniendo la siguiente gráfica

El vértice de la parábola se calcula, como bien sabemos, de la siguiente forma:
V(xo,yo) siendo xo=-b/2a=0,556=13:23; yo=f(xo)=84cm
Con estos resultados experimentales
Resultado experimentales Saldaña
| Altura Solar Mediodía | Hora solar |
| 50°12' | 13:23 |
En Internet hay una página que nos calcula los datos exactos, tanto de la altura como de la hora solar, sólo hay que introducir el día y la latitud y longitud de Saldaña (Latitud: 42°32' N y Longitud 4°44' W). La página es la siguiente: http://www.geocities.com/xgarciaf/java/orto.htm. Según esta página la altura solar y hora al mediodía ese día es:
Resultado Reales Saldaña
| Altura Solar Mediodía | Hora solar |
|
49°50' |
13:25 |
Para calcular el radio terrestre necesitamos los datos de otro instituto, de entre los muchos calculados hemos tomado los datos de los institutos de Málaga (Latitud 36° 40' y Longitud 4° 29' W) por dos razones: 1) La longitud es semejante a la de Saldaña 2) Es la ciudad de España más alejada a Saldaña
En Málaga los resultados son los siguientes:
Resultado Reales Málaga
| Altura Solar Mediodía | Hora solar |
|
55°50' |
13:24 |
distancia Málaga-Saldaña=677km
De esta forma la diferencia de latitud experimental entre Saldaña y Málaga es a= 55°50'- 50°12'=5°38'=5,63° y el Radio de la Tierra calculado es por tanto:
Resultados experimentales
![]()
![]()
Resultado real
R=6.378km
Error cometido: 8%
En la página de astronomía 2009 podemos ver los resultado de todos los institutos: resultados
Más enlaces:
http://www.astrored.org/usuarios/xgarciaf/orto1.htm