RETOS MATEMÁTICOS DE "EL PAÍS"

    El periódico "El Pais" esta teniendo una bonita iniciativa: plantear retos matemáticos y sortear para los acertantes una colección de libros matemáticos.

    Estoy recoleccionando los restos y las soluciones que da el periódico y las que voy mandando yo:

                                                                       

 1er reto: Un problema de ciudades y carreteras

Solución                  

 

Mi solución: Mi solución es la misma que se describe, aunque he visto otra muy original (http://manueltorrestorres.blogspot.com) que se puede ver en el siguiente gogledoc: solucion

 

2º Reto: Una hormiga amenazada                                                                                                            Solución:

   

Mis soluciones: Plantee el problema de dos formas,

1) Totalmente teórica del teorema de grafos, (An nos da el numero de caminos con n aristas y por tanto con probabilidad (1/3)n.). Para calcular An diagonalice la matriz.

2) Por la simetría del grafo se plantea un sistema que se resuelve fácilmente.

 

3er Reto: Cuadro mágico de productos                                                                                                            Solución:

 

Mi solución:  Tenemos que buscar 8 ternas de productos que den el mismo resultado, 3 filas, 3 columnas y 2 diagonales. El problema es que estos están relacionados pues cada número tiene que pertenecer a dos ternas (sino esta en ninguna diagonal) o a 3 ternas (si está en una diagonal) y el del medio a 4 ternas (está en las dos diagonales).

Nos plantean un número conocido, el 15 que como está en el centro pertenece a 4 de las 8 ternas. Después de meditar he generalizado el problema de la siguiente forma:

Si a y b son dos números enteros positivos cualesquiera el siguiente cuadrado es mágico: (todos los productos son a3·b3)

b a2·b2 a
a2 a·b b2
a·b2   1 a2·b

En nuestro caso a·b=15, luego a=3 y b=5:

5 225 3
9 15 25
75   1 45

Nota: si a todos los números les multiplicamos por un mismo número sigue siendo válida la solución.

 

 

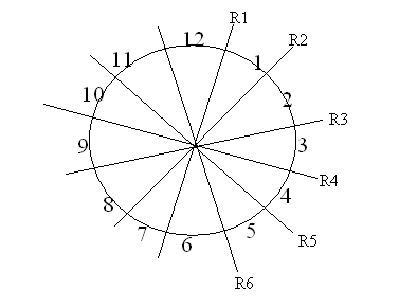
4º Reto: El reloj de dos colores                                                                                                                   Solución:

   

Mi solución: parecida a la dada por el video pero más matemático:

    Hay  6 posibles rectas, la idea es demostrar que al menos una de ellas sea la solución (3 rojas a cada lado). Veamos que así es por reducción a lo absurdo. Cojamos una recta cualquiera, por ejemplo la R1. Si esta recta no fuera la solución que dejara 3 rojas a cada lado (supongamos que n para el semiplano que gira en sentido horario (1,2,3,4,5,6) y m al otro (7,8,9,10,11,12), tal que n+m=6), miramos la siguiente, puede ocurrir:

  1. Mismo numero de rojas (coge una roja y deja otra, o no coge ni deja ninguna roja)
  2. Una roja más (coge una roja y deja una blanca)
  3. Una roja menos (coge una blanca y deja una roja)

    Cuando recorremos las 6 rectas debido a la periodicidad llegamos otra vez a la primer recta R1, pero desde el punto de vista  del giro lo que era antes el semiplano horario a hora es el otro (7,8,9,10,11,12). Se cumple entonces que ahora m pasa a ser n y al revés. Si m ¹n  (es decir la recta R1 no era la solución) tenemos que pasar de m rojas a n rojas. Como m+n=6 supondremos que m>3 y por tanto n<3; como el numero de rojas sólo aumenta o disminuye de uno en uno para pasar de m>3 rojas a n<3 rojas tiene que pasar por un momento en que valga 3, y esta recta será la solución.

 

 

5º Reto: Un Pais de Palillos                                                                                                                 Solución: