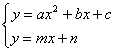
Tipo 3

Consideraremos los sistemas no lineales formados por dos ecuaciones de la forma: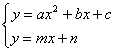

Las dos ecuaciones del sistema, como sabemos, la primera una parábola y la segunda una recta.

La solución grafica de este sistema serán los puntos que resultan de la intersección de la parábola y la recta. Puede tener, 0, 1 o 2soluciones.

Para resolver el sistema el método mas sencillo es el de igualación.(A veces la recta no esta despejada la y)

Veamos un ejemplo: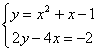

Despejamos la y de la segunda ecuación: y=-1+2x

Igualando la y :  x²+x-1=-1+2x à x²-x=0  àx=0 y x=1

Soluciones:

x=1à y=1   P(1,1)

x=0à y=-1  P(0,-1)

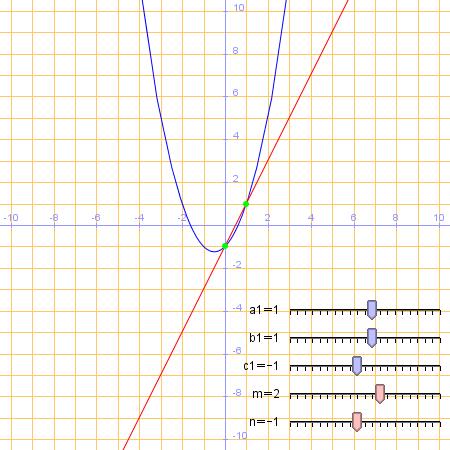
En la grafica que se abre puedes modificar los parámetros a, b y c de la parábola y la pendiente (m) y la ordenada de la origen de la recta (n)

Ejercicio: Resolver los siguientes sistemas, representar y comprobar las soluciones con la grafica modificando los parámetros a,b,c, de las parabolas y m y n de la recta.

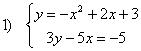
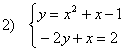
Aprende a utilizar el Wiris y el Derive para resolver sistemas y resuelve los dos sistemas