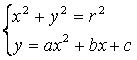
Tipo 1
Consideraremos los sistemas no lineales formados por dos
ecuaciones de la forma: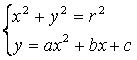
La primera ecuación del sistema, como sabemos, es la de una circunferencia de radio r.
La segunda ecuación es una parábola.
La solución grafica de este sistema serán los puntos que resultan de la intersección de la circunferencia y de la parábola. Puede tener, 1, 2, 3 o 4 soluciones.
Para resolver el sistema sustituimos la y de la segunda ecuación en la primera, obteniendo una ecuación de 4º grado.
Por sencillez trabajaremos con la parábola cuando b=0 (y=ax2+c), y por tanto el vértice situado en el eje OY V(0,c). Este sistema también se puede resolver por reducción, eliminando x2 entre las dos ecuaciones.
Veamos un ejemplo: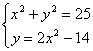
Método 1 (por sustitución):
x2+(2x2-14)2=25
à
x2+4x4-56x2+196=25
à4x4-55x2+171=0
(bicuadrada x2=t, x4=t2)à
4t2-55t+171=0
à
t1=9, t2=19/4
à
x=±3, x=
Soluciones:
1) S1: x=3 à y=2·32-14=4 S1(3,4)
2) S2: x=-3 à y=2·(-3)2-14=4 S2(-3,4)
3)
S3: x= à
y=2·()2-14=-9/2
S3(,-9/2)
4)
S4: x= à
y=2·()2-14=-9/2
S4(,-9/2)
Método 2 (por reducción):
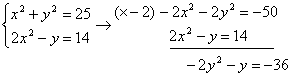
2y2+y-36=0 à y1=4, y2=-9/2
Soluciones:
1) S1 y S2 : y=4 à 2x2-4=14 à x2=9 à x=±3 à S1(3,4) y S2(-3,4)
2) S3 y S4: y=-9/2 à2x2+9/2=14 à x2=19/4 à x=± à S3(,-9/2), S4(,-9/2)
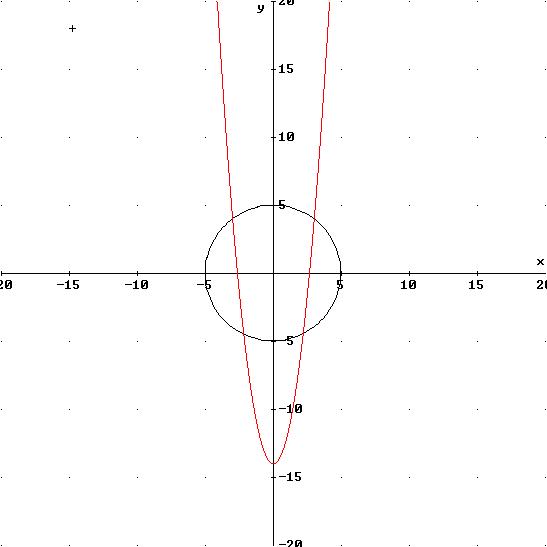
En la grafica que se abre puedes modificar los parámetros a, b y c de la parábola y r=radio de la circunferencia y ver las graficas y las soluciones del sistema.
Ejercicio: Resolver los siguientes sistemas, representar y comprobar las soluciones con la grafica modificando los parámetros a,b,c y r.
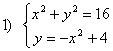
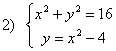
Aprende a utilizar el Wiris y el Derive para resolver sistemas y resuelve los dos sistemas