Inecuaciones ecuaciones de segundo grado

Las inecuaciones de segundo grado son expresiones de la forma:

1) ax²+bx+c>0

2) ax²+bx+c<0

3) ax²+bx+c≤0

4) ax²+bx+c≥0

Para resolución de esta inecuación los pasos a seguir son los siguientes

1) Resolver la igualdad ax²+bx+c=0. Puede ocurrir:

    a) Dos soluciones {x₁,x₂}. Estudiamos el signo de la expresión en los intervalos (-¥,x₁), (x₁,x₂) y (x₂,¥)  

    b) Una solución {x₁}. La función será siempre positiva o negativa menos en x₁ que vale cero

    c) No solución. La función será siempre positiva o negativa en R

2) Calculamos los intervalos donde cumpla la inecuación.

Veamos un ejemplo:x²-4≥0

1) x²-4=0 ® x=2, y x=-2

2)  Solución: (-∞,-2] È [2,∞)

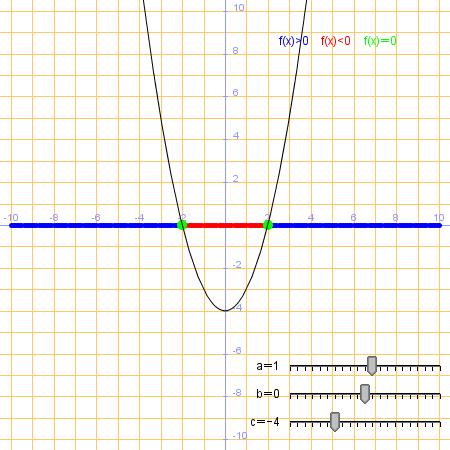
Para ver la resolución grafica representar la parábola y=ax²+bx+c, la parte que esta por encima del eje OX será el intervalo que cumple ax²+bx+c>0, la que esta por debajo del eje OX es el intervalo que cumple ax²+bx+c<0; los puntos de corte con el eje OX son los valores de x que cumplen la igualdad f(x)=0.

En nuestro ejemplo veamos la grafica:

En la grafica que se abre puedes modificar los parámetros a, b y c de las parábola e interpretar las soluciones de las inecuaciones

Ejercicio: Resolver las siguientes inecuaciones, representar y comprobar las soluciones con la grafica modificando los parámetros a,b,c de la parábola

1)     x²+3x-10>0

2)     -x²-10x-25≤0

3)     x²+x+10<0

Aprende a utilizar el Wiris y el Derive para resolver inecuaciones